A Guest Post About High Sample Rates
I received an email on the 13th from Fritz Fabig, an engineer at B&W that British high end speaker and equipment company. He wrote concerning the MQA posts I wrote and the general area of sampling, timing, and the sinc function. I’m going to admit to being somewhat out of my league with the information he included in his email, but I think there’s merit to his position. I asked him if I could reprint the email and figures and he gave me permission. He did ask that I try to clean up the English…which I have tried to do. Here’s his email:
Hi Mark
You wrote a couple of very interesting posts recently. Your post on MQA provoked a discussion about sampling theorem and with the December 12th Stereophile online article about the worlds ‘first’ DXD download store, it’s even more important to educate and inform music enthusiasts about digital technologies correctly, as you do with your site.
The question about human hearing in the time domain leads to the assumption that higher sampling rates than 96k might be useful or even mandatory to provide a level of time accuracy within the digital domain. This is wrong in my opinion.
a) A time shift of for example of 10 microseconds (traveling of sound pressure around the human head) results in a time or phase shift of the signal, which may have a frequency spectrum of normal instruments (up to 40k, if we consider ultrasonics too). To cover this frequency spectrum 96k is sufficient. The time shift between the channels (either our ears or due to spaced mikes) results in a different form of the shell curve at a specific time point, as we have a phase shift between the channels.
b) A lot of people, including many professionals in the audio industry, believe that information between the samples is lost at 96 kHz, which isn’t true. Therefore according to their way of thinking in order to capture these tiny time shifts ultra high sample rates are necessary.
c) In order to get this sorted right and prove that no information between the samples is lost and that these tiny time shifts are captured and reproduced accurately, we have to look at sampling theorem and signal processing on a technical level. Here two useful links about this topic:
Dan Lavry: “Optimal Sampling Rate for Quality Audio” Link
Monty Montgomery from xiph.org: “24/192 Music Download and why the make no sense” Link [NOTE: I’m not in agreement with Monty on some of his contentions]
You are maybe already aware of these papers/videos
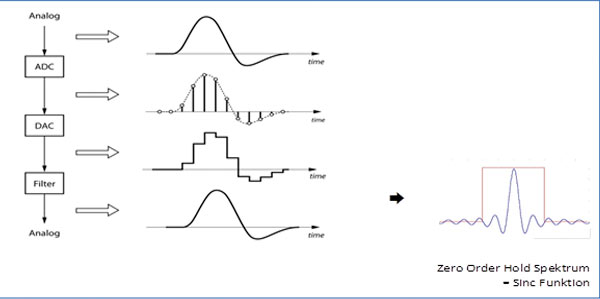
d) One important point for proper understanding of the digital concept is the sinc function, seldom mentioned in discussions and papers. We have created a paper to educate our dealers, where we try to convey this rather complex topic in a way, that people with no deep background in mathematics and electrical engineering may understand the essentials. Besides human hearing abilities and frequency range of instruments, the key points in this paper are the transition from time continuous analog to a time discrete digital format and vice versa.
Figure 1 – The digitization process top to bottom and the “Zero Order Hold Spectrum” or Sinc Function.
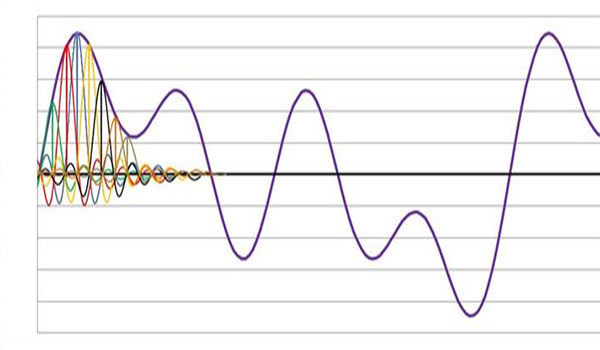
The key point for us is that the Zero Order Hold Spectrum contains the sync function (theory: sample is multiplied by sinc function ![]() . As a next step we see how samples & sinc reconstruct the analog signal with all information including those between the samples and also complex waves (shell curve):
. As a next step we see how samples & sinc reconstruct the analog signal with all information including those between the samples and also complex waves (shell curve):
Figure 2 –
Please refer for this also to Dan Lavry’s white papers: Link
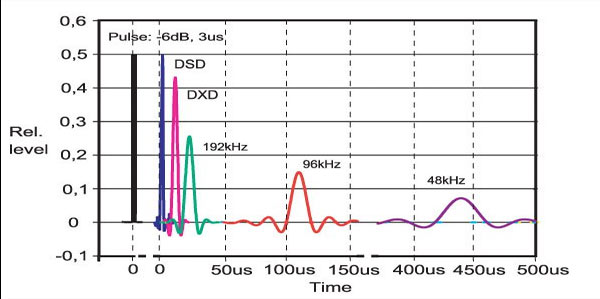
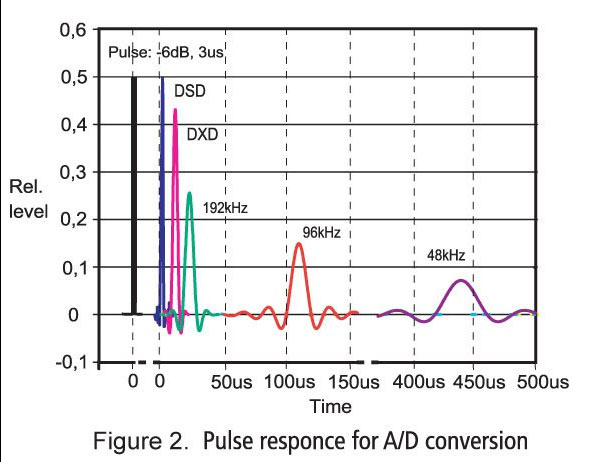
e) The sinc pulse is another example, how people can misunderstand a technical term or deliberately abuse it to try to prove their marketing hocus pocus. This new DXD download portal, Promates Music HD Music Store, features a chart with sinc pulses to prove that higher sampling rates are beneficial: here the Link and the chart:
Figure 3 – Pulse or transient response for ADC
The same chart is available on Merging Technologies website, conveying the same nonsense. In order to accurately reconstruct the source signal, it’s essential and mathematically correct that the lower the sampling rate the wider the sinc pulse has to be. If this wouldn’t be the case, the concept wouldn’t work AND the 3 microsecond pulse represents a frequency of 333.3 khz. That’s completely taken out of the context and is absolutely misleading. All this to get $10 extra for a lot of zeroes. Further, the sinc pulse is a mathematical element and there is no direct or proportional relation between pulse width and the ability of a digital system to convey transients and reproduce phase and time shifts. This is only depending on the two parameters S/N Ratio (dynamic) and bandwidth.
Conclusion: It’s obvious that marketing departments can construct graphics and materials that support case when taken out of the context and rearranged to match their story, a story which is unfortunately is pure nonsense.
All the best from Switzerland
Fritz
B&W Group (Schweiz) GmbH
+++++++++++++++++++
I’m still looking to raise the $3700 needed to fund a booth at the 2015 International CES. I’ve received some very generous contributions but still need to raise additional funds (I’ve received about $2400 so far). Please consider contributing any amount. I write these posts everyday in the hopes that readers will benefit from my network, knowledge and experience. I hope you consider them worth a few dollars. You can get additional information at my post of December 2, 2014. Thanks.

Interesting. I was talking about this topic with a friend the other day, and we began wondering if DACs actually do approximate the Sinc function when filrering. I think its time for me to read those referenced papers and read up on some theory (and measurements) of DACs.
At last an industry person, albeit an engineer rather than a marketing man, joins in to tell the truth. I’ve been trying to convey the same since my first comment in this blog, a few posts ago. The so called ‘time domain considerations’ are a red herring joining the ‘not enough samples to produce a smooth line’ one in the quest for more $$ for the industry. The sinc function is the mathematical brickwall low pass filter btw.
PS. There ARE well known and discussed practical engineering problems (i.e. introduction of distortion) in implementing the filter in electronic DA converters, which can be overcome or mitigated to very high frequencies by internally oversampling to very high rates, but this should neither be taken as a limitattion of the theory nor as justifications that higher orifginal sampling rates are required to avoid information loss below the Nyquist frequency.
PS2. I just read this http://www.hifiplus.com/articles/mqa-its-about-time/?utm_campaign=Hi-Fi%2B+Weekly+Emails&utm_medium=email&page=2&utm_source=email-323, an attempt from someone to provide a plausible explanation of what MQA is all about. I’m not commenting on all the neuroscience stuff, because it is IMO unimportant in the context of our discussion here. The important bit to notice is the quote ‘…In overly-simplistic terms, when we sample a piece of music in PCM, we work to the frequency domain and bring the time domain along for the ride. Traditionally this has been no problem, because the response time for a human brain to process tones is slower than any potential inter-sample timing errors…’ Once again the author demonstrates an inexcusable lack of understanding of how the A-D-A conversion chain operates, when he talks about inter-sample timing errors… I’m sure we are going to hear much more of this mumbo-jumbo in the very near future.
I’ll have to take a look. Running right now.
PS3. Below quote is from Dan Lavry’s excellent paper http://lavryengineering.com/pdfs/lavry-sampling-theory.pdf
summarizing what I have been pointing out all along, namely that the distinction between frequency and time domains is wrong since they are one and the same thing. The only difference is the ‘window’ used to look at it. People pointing to time domain considerations whoch are not addressed by frequency domain processing either do not understand signal processing theory and Fourier transforms or do it to intentionally mislead.
‘So if going as fast as say 88.2 or 96KHz is already faster than the optimal rate, how can we
explain the need for 192KHz sampling? Some tried to present it as a benefit due to narrower impulse response: implying either “better ability to locate a sonic impulse in space” or “a more analog like behavior”. Such claims show a complete lack of understanding of signal theory fundamentals. We talk about bandwidth when addressing frequency content. We talk about impulse response when dealing with the time domain. Yet they are one of the same. An argument in favor of microsecond impulse is an argument for a Mega Hertz audio system’ (i.e. an audio system capable of delivering MHz frequency response…)
Now pls. tell me to finally shut up and do something more constructive, like going to work. It’s morning here.
Great post!
If I understood a word of it, it would be even better I’m sure. LOL
Hej Mark,
Once again, greetings from the far north of Sweden, where all 9 million of us read your daily posts with joy in our hearts!
Just a quick note… I have commented a few times how important it is to us readers that your message is disseminated to us hoi polloi. I know you fear repeating the facts of sound reproduction, but this stuff cannot be repeated often enough! This particular post seems to me a break through of some sort… a quote from one of the insiders of international commercial music who would have every reason to remain silent, instead not only openly supports your mission, he engages scientifically to help dispel the myths of personal opinion or, worse, subjective truth in recorded sound reproduction.
We in Sweden regard this as a sign that you are indeed being heard world-wide and that your work matters a lot and to many! Keep it up, fight the power and let us all bask our selves in the sufficient warmth of 96 kHz!!
vänliga hälsingar,
bill
I believe this article is explaining why sub-10ms time shifting adds nothing.
I must admit to not understanding the points being made.
If the ear can detect 5ms difference as to when sound arrives, surely a higher sampling rate must help? Logically, this should suggest at least 200KHz – so, surely anything around this or a greater sampling rate must be good?
Perhaps, someone can explain this using non-technical language?
Thanks
Julian…I will write about this and try to get it down in plain English. The fact is that we don’t need any higher than 96 kHz/24-bits.
Julian,
the essence is that what you call time shift (in the time domain) is the same as a phase shift in the frequency domain. What one may call an impulse in the time domain is the same as a rectangular wave of very high frequency in the frequency domain. There are NO phenomena in the time domain which are not reflected in the frequency domain. The theory goes that ALL information, including phase shifts, impulses or whatever have you that lie BELOW half the sampling frequency can be accurately captured and represented. There are no strange phenomena that happen below that frequency that are not captured. So the question remains the same. How high a frequency can be heard or sensed by a person? Asking for a 200Khz sampling rate is exactly equal to suggesting that humans can hear frequencies up to 100Khz. One can not have it both ways (i.e. agree that about 20Khz is the limit of human hearing ,which we generously expand to about 40Khz, while at the same time suggest that there are ‘phenomena’ which happen at 100Khz which need to be captured because they can be ‘heard’). Now it is easier to convince me that you are a bat or you have radar ears than convince me that you aren’t but for some reason such a high samplng rate is required. One cannot have his pudding and eat it too.
Just to add, in case this is still misunderstood, that ANY ‘time shift’ of a wave, which means any phase shift, however short that may be (meaning however small the phase shift) is ACCURATELY captured as long as the wave itself can be captured (i.e. is below half the sampling rate). Translating a time shift to frequency is NOT correct. Time shifts should be translated to phase shifts. Sampling provides CONTINUITY of capturing as long as what is captured is below half the sampling frequency.
This site is a wonderful resource for countering the spurious claims out there in the hi-end audio world, not only for Mark’s yeoman work in generating his daily columns (SO appreciated!), but also for such intelligent responses as Nik’s. My only question is, how can so many in the hi-end world be so deluded? – this DSD worship (not least because of its “superior transient response” – a claim you encounter often on places such as SA-CD.net) is sheer madness! (Again, this is not to say that some great DSD recordings haven’t been produced, but jeez. . . !)
The truth is out there but many refuse to acknowledge it.
Julian, if I may have a try in plain English. If you sample a signal at 10 kHz or at 100 kHz, the latter may get the *shape* of the signal more accurately (because some of the signal is at frequencies too high for the 10 kHz sampler), but it won’t get the *position* of the signal on the time axis any more accurately — and that position is the ‘timing’. In fact, even at 10 kHz or even 1 kHz sampling, the timing of a digital sampling and reconstruction system is within a few nanoseconds.
Humans are actually very poor at detecting the timing of a single channel of audio, but we are good at detecting the relative timing of two channels. Digital audio can *get* that relative timing very, very accurate no matter what the sampling rate.
cheers
Nik, Are you saying that there is a link between the freq. and signal delay between our two ears?
That is, although we can recognise a sub-10ms delay, this is irrelevant as it only applies to frequencies of 100Khz (1000/10).
If so, given most people can’t hear above (15-20khz), then ignoring all other issues, does this mean that having a sampling rate of more than, say, 40khz doesn’t make sense when is comes to signals delays only?
How do we then know that the brain can recognise 5ms delays, if we cannot hear the source?
Linked Comment:
I have read ‘music energy’ has been measured to around 100khz. Surely then, a 96khz sampling is too low, unless you are okay with the principle that some of the music is removed?
I understand that such an imposed ceiling is one of the main concerns regarding DSD – although I suppose, this argument begins to dissipate with DSD256.
I do not mind if a recording is in DSD or PCM. Actually, most of the time my choices are determined by the recording (classical piano).
However, previously, I would typically buy a 192khz rather than 96khz versions because of the higher ‘music energy’ ceiling and the improved resolution of the signal delay (which appears to be untrue?).
(I also admit to buying 384khz tracks from 2l… and yes, they sound magnificent…)
Mark, I also welcome your non-technical response, if at all possible, regarding our spacial awareness of the sound source/the brain’s capacity to recognise signal delays.
Thank you.
Check out today’s post. I purchased a new DXD recording from Promates and posted the spectrogram. It’s very interesting and shows the idiocy or 352.8 kHz audio…everything above 45 kHz is noise.
Julian, as I tried to convey, the signal delay is manifested as a phase shift not a frequency change. Such a phase shift is represented in a freq diagram by the wave being displaced to the right on x-axis (time axis) of a frequency against time plot. Absolutely nothing to do with frequency in this case. A pulse on the other hans is manifested as a short square wave. If this pulse in below the Nyquist freq then is it going to be sampled correctly, otherwise it is not as with any wave.
Hi Julian, the way they tested to find that we can detect a timing change of as low as 5 micro seconds (5 us), was to play an audible signal through 2 channels so that a phantom source was located between the speakers (or headphone drivers), then delay one channel very slightly until the subject can barely detect if the phantom source has moved. It has nothing to do with high frequencies; one can run the test with any frequency that we are good at locating — pretty much anything over about 500 Hz.
And, as I explained yesterday in another comment above, digital audio gets the timing of the two channels right to within a few nanoseconds (a thousand times faster than 5 us), no matter what sampling rate is used. So, it is a non-issue, i.e. it is not a reason to up the sampling rate.
cheers
Grant, Mark, Nik – thanks!